Im Oktober 2005 ging folgende Meldung um die Welt: "Mount Everest nach chinesischen Angaben nicht so hoch wie angenommen! Nach den Daten einer Expedition vom Mai betrage die Höhe über dem Meeresspiegel 8.844,43 Meter, so der Chef des chinesischen Vermessungsamts. Eine US-Messung hatte 1999 eine Höhe von 8.850 Metern ergeben, eine chinesische 1975 eine Höhe von 8.848,13 Metern.

Was nun? Fast im Jahrestakt neue "Höhen" des Everest, neue Erkenntnisse, neue Verwirrung. Wie hoch ist nun der Everest tatsächlich? Und wie misst man seine Höhe?

Faktoren für die Berechnung von Berghöhen

Welche Faktoren sind nun wichtig zur Vermessung und Berechnung von Berghöhen? Zum ersten natürlich die Meereshöhe, weiters die Genauigkeit und Auflösung des Mess-Equipments und des Mareographen, auf den die Messung referenziert wird, und schließlich die Schneehöhe am Gipfel eines Berges, die sich im Laufe eines Jahres oft ändert.

• Mareographen
  
  Jede Höhenmessung bezieht sich auf eine definierte Referenzfläche, den langjährig gemittelten Pegelstand des Meeresspiegels. Für Westeuropa ist dies meist Normalnull (NN), der Pegel von Amsterdam. Andere traditionelle Referenzflächen sind u. a. die Pegel von Genua, Königsberg (Kaliningrad), Kronstadt (Russland) und Marseille.
  Der Unterschied zwischen "Normalnull" und "Meter über Adria" beträgt – je nach Lage im regionalen Höhennetz – bis zu 30 cm. Mareographen zeichnen rund um die Uhr die Meereshöhe auf. Die Alpenvermessung der Italiener bezieht sich auf den Mareograph in Genua, die Österreichische auf Triest und die Schweizer Geodäten referenzieren auf ein Mittel zwischen Genua und Bordeaux. Auch hier unterscheiden sich die Messungen von Italienern und Schweizern um bis zu 20 cm.
  Daher kann man sich jetzt vorstellen, warum die Messungen der Chinesen (Mareograph in Quingtao) mit denen der Nepalesen (Karachi - Indischer Ozean) kaum übereinstimmen können, wenn etwa 6000 km zwischen den beiden Referenzpunkten liegen!

• Ellipsoid und Geoid
  
  Die Differenzen zwischen den Meereshöhen resultieren aus der Tatsache, dass die Masse im Erdinneren nicht gleichmäßig verteilt ist. Das Wasser passt sich natürlich an und ist im Gleichgewicht. Denkt man sich die Meeresoberflächen zueinander verbunden, so entsteht ein Geoid. Die entstehende Oberfläche ist völlig unregelmäßig. Für GPS wird ein vereinfachtes Modell - das Ellipsoid - verwendet (Äquatorachse, Polachse und ein Faktor für die Erdabplattung). Der Unterschied ist die Normale zwischen Ellipsoid und Geoid und dieser kann mehrere Meter betragen.
  1992 wurden von der chinesischen Seite 25,14 Meter für den Everest berechnet. Nach etlichen Korrekturen werden heute üblicherweise 28,74 Meter angenommen. Sowohl das elliptische Modell als auch das Geoid sind mittlerweile sehr exakt anzugeben.

• Würde man den heute üblichen Wert heranziehen, so würde die Höhe des Everest nach der chinesisch-italienischen Vermessung (1992) 8852,25 Meter betragen. 1999 wurde die Angabe auf 8850 Meter korrigiert. Heute weiß man, dass diese Differenz mit unterschiedlichen Schneehöhen begründet werden kann.

Daher muss bei der Höhenvermessung die Felsoberfläche mit einbezogen werden.

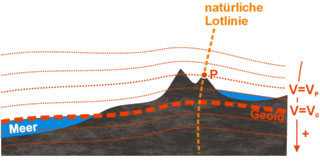
Zusammenfassung:

• Um die Höhe eines Berges zu bestimmen, braucht man den Nullpunkt (Meereshöhe). Verbindet man die über lange Jahre gemittelten Nullpunkte auf der ganzen Welt, ergibt sich ein unförmiges Ei - das Geoid.
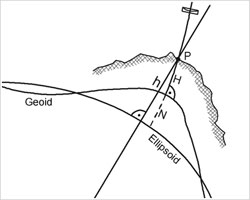
• GPS basiert aber auf einem idealisierten mathematischen Modell, dem Ellipsoid. Das Geoid kann vom Rotationsellipsoid bis zu ±100 Meter abweichen. Hat man also mittels GPS einen Höhenwert ermittelt, muss man die Differenz zwischen Geoid und Ellipsoid berücksichtigen, um eine exakte Angabe machen zu können.
• Schneelage: Einen reproduzierbaren Wert kann man nur dann angeben, wenn man die Schneehöhe mitberücksichtigt bzw. die Höhe des Felsen misst.

Wie hoch ist der Everest?

Die unterschiedlichen Werte bei der Vermessung des Everest in den 90er Jahren rühren daher einerseits aus der Bestimmung des Geoids und andererseits aus den unterschiedlichen Schneelagen her.

Everest - Mai 2004

Für die Messung im Mai 2004 wurde ein GPR (Ground Penetrating Radar) mit einem GPS (Global Positioning System) gekoppelt (Das Gerät wiegt etwa 4 kg inklusive Batterien, wobei deren Lebensdauer bei ungefähr 7 Stunden liegt). Am Gipfel wurden 8 Radarprofile mit Abständen zwischen 2 und 4 Metern aufgenommen, wobei die Profile 1,2 und 3 in unmittelbarer Nähe des Gipfels lagen.

Claudio Bastrentaz beim Messen mit dem GPR

Radar-Profile am Gipfel

Aus diesen Profilen wurden Computermodelle der Schnee- und Felsoberfläche generiert, wobei die Schneehöhe zwischen 285 und 370 cm angegeben werden konnte.

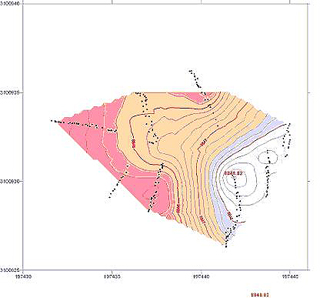
Felsprofil

Die Ergebnisse der Everestvermessung 2004

1) Der absolut höchste Punkt wurde mit 8852,12+-0,12 Metern ermittelt. An dieser Stelle war der Fels darunter 8848,40 Meter hoch, Schneehöhe daher 3,7 Meter.

2) Die höchste Felspunkt lag 8848,82+-0,23 Meter und etwa 1,15 Meter nördlich vom oben genannten Punkt.

Die größte Ungenauigkeit fällt dem Radargerät zu, da die Ausbreitungs-geschwindigkeit der Radarstrahlen im Schnee an Ort und Stelle kalibiriert werden müsste. Hier wird ein möglicher Fehler von bis zu 20 cm angegeben. Die Fehler der GPS-Daten liegen im Bereich von wenigen Zentimetern; auch eine Berechnungsungenauigkeit bei der Auswertung der Radardaten wurde berücksichtigt.

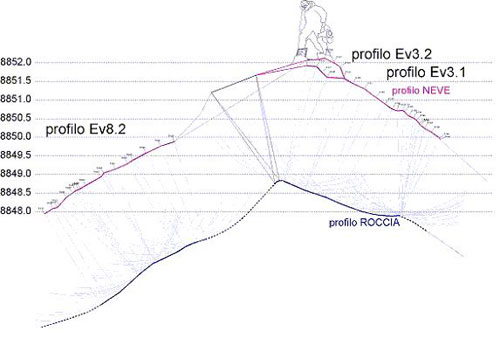
An dieser Stelle möchten wir Herrn Giorgio Poretti von der Universität in Triest herzlich danken. Er hat uns eine Menge Infos zukommen lassen und die Bilder zur Verfügung gestellt.